用語解説　幾何公差編②

金属加工、機械加工における、専門用語「幾何公差編２」をわかりやすく解説致します。
機械加工ビギナーの人にとっては加工用語がなかなか覚えられない、意味が分からないものが多い事があるのではないでしょうか。
加工部品の専門商社がまとめた〈幾何公差の専門用語集〉で理解を深めていただけるコンテンツとなっています。

面の輪郭度

面の輪郭度とは、幾何学的に正しい曲面からのひらきの誤差の許容値を示す。線の輪郭度とは違い指定の面全体が対象となる。例えば、面の輪郭度0.1の場合、2つの幾何学的に正しい曲面の間隔を0.1mmとし、その間隔に対象物の曲面部分が収まっている場合は面の輪郭度0.1以内となる。

直角度

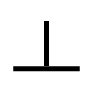
直角度とは、基準となる面や線（データム）から対象となる面や線が直角であるかどうか、そのひらきの誤差の許容値を示す。例えば、直角度0.1の場合、平面の上にφ0.1の円筒を立ててイメージすると分かりやすい。平面Aをデータム（基準）として、対象箇所の “倒れ” がφ0.1の円筒内に収まっていれば直角度0.1といえる。

傾斜度

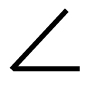
傾斜度とは、基準となる面や線（データム）から対象となる面や線が指定の角度であるかどうか、そのひらきの誤差の許容値を示す。指定する単位は角度ではなくミリ（mm）である。例えば、傾斜度0.1の場合、基準となる平面や線をデータムAとして、2つの幾何学的に正しい面や線の間隔を0.1mmとし、その間隔に対象となる面や線が収まっている場合は傾斜度0.1といえる。

位置度

位置度とは、基準となる面や線（データム）から理論的に正確な位置にあるか、そのひらきの誤差の許容値を示す。例えば、位置度φ0.1の場合、寸法通りの位置に開けた穴の中心点がφ0.1の幾何学的に正しい円の中に収まっている場合、位置度φ0.1といえる。

同軸度

同軸度とは、円筒など対象物の中心軸が基準となるデータム軸からどれだけひらいているか、その許容値を示す。
例えば、同軸度0.1の場合、対象物の真ん中を通っていると仮定するデータム軸線を中心に、実際の軸のズレがφ0.1の円以内に収まっていれば、同軸度0.1といえる。

同心度

同心度とは、円を平面でみたときに、対象となる円の中心点と他の円の中心点のひらきの許容値を示す。
外形側の大きな円と内径側の小さな円の中心点が、指示された公差数値、0.1の場合ならφ0.1の円内に収まっている場合、同心度が0.1といえる。

対称度

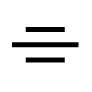
対称度とは、データムに対して互いに対称となる部分が正しい位置からどれだけひらいているのか、その許容値を示す。例えば対称度0.1の場合、対称度の指示がある部分と対象となるところが、データム（基準）と平行で0.1mm間隔の幾何学的に正しい2枚の平面の間に収まっていると対称度0.1といえる。

円周振れ

円周振れとは、主に回転する部品に指示される公差。例えば、段付きシャフトの大径側の円周振れを評価する場合、小径側の中心点を基準にして円筒を回転させ、大径側の円の形が変位する許容値を示す。円周振れ0.1の場合、データム軸と同軸となる0.1mm幅の2つの幾何学的に正しい円の間隔に回転する大径側の円の表面（変位する幅）が収まっていれば、円周振れ0.1だといえる。

全振れ

全振れとは、主に回転する部品に指示される公差。例えば、段付きシャフトの大径側の全振れを評価する場合、小径側の中心点を基準にして円筒を回転させ、大径側の円筒の形が変位する許容値を示す。円周振れの場合、円を二次元で捉え表面の振れが許容値内であるかをみる。対して全振れの場合、評価対象となる円筒部分全て（ここでいう所の大径側円筒部全て）となる。全振れ0.1の場合、データム軸と同軸となる0.1mm幅の2つの幾何学的に正しい円筒の間隔に回転する大径側の円の変位する幅が収まっていれば、全振れ0.1だといえる。